"Control Loop Design for Linear and Switching Power Supplies" is the latest book by Christophe Basso, a well-known columnist in the field of Power Electronics. This comprehensive work provides engineers with essential knowledge on compensating and stabilizing control systems. It includes an excerpt from the book discussing stability standards, which are crucial for understanding how to design reliable power supply systems.
In the electronics domain, an oscillator is a circuit that generates a self-sustained sinusoidal signal. These circuits often rely on inherent noise within the system to initiate oscillation. At power-up, the noise level increases, triggering the start of the oscillation process. Such a configuration can be broken down into basic components as shown in the figure. As you can see, this setup closely resembles the structure of a typical control system.

Figure 1: The oscillator essentially acts as an error signal that does not interfere with the main output signal of the control system.
In our example, instead of relying on noise, the excitation input is the voltage Vin, which serves as the starting point for the oscillator. The direct path consists of the transfer function H(s), while the feedback path contains the G(s) block. To analyze this system, we first derive its transfer function based on the relationship between the output voltage and the input variable:

In this equation, the product G(s)H(s) is referred to as the loop gain, denoted as T(s). For the system to become a self-excited oscillator, it must produce an output even when the input is removed. This requires satisfying two conditions:

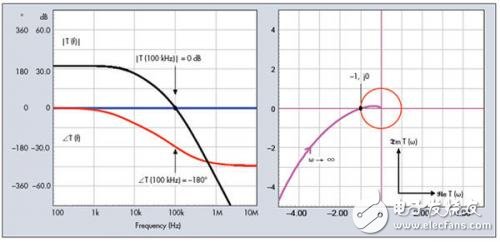
Figure 2: Oscillation conditions can be visualized using Bode or Nyquist plots.
When these two equations are satisfied, the system reaches steady-state oscillation, known as the Barkhausen criterion, proposed by German physicist Barkhausen in 1921. In a control system, this means the correction signal no longer opposes the output but returns in phase with the same amplitude as the excitation signal. Equations (6) and (7) represent the loop gain curve in a Bode plot, crossing the 0 dB axis with a 180° phase lag. In the Nyquist plot, the loop gain's imaginary part is plotted against the real part at a specific frequency, and the point -1 + j0 represents the condition for oscillation. Figure 2 shows two curves that meet the oscillation criteria. If the system deviates slightly—due to temperature changes or component variations—the oscillation either decays exponentially or grows until it hits the power rails. In oscillator design, engineers aim to minimize the gain margin so that oscillation conditions are met under various operating conditions.
**Stable Condition**
As you know, the goal of a control system is not to create an oscillator. Instead, we want the system to respond quickly, accurately, and without oscillation. Therefore, we must avoid configurations that lead to instability or divergence. One approach is to limit the frequency range where the system reacts. By definition, the bandwidth refers to the frequency at which the closed-loop gain drops by 3 dB. This bandwidth indicates the range of frequencies where the system performs well, following setpoints or suppressing disturbances. During the design phase, we don't directly control the closed-loop bandwidth but instead focus on the crossover frequency fc, which is related to open-loop analysis. Although they are usually considered similar, they are not exactly the same, and their relationship depends on certain conditions. However, they are close enough to be used interchangeably in many discussions.
We have seen that the open-loop gain plays a key role in the system’s behavior. When |T(s)| > 1, the system operates in a dynamic closed-loop mode, compensating for disturbances or responding to setpoint changes. However, there are limits to how fast the system can react. It needs sufficient gain at the frequency of the disturbance. If the disturbance occurs too rapidly, the system may not have enough gain to respond effectively, resulting in a sluggish response. So, is infinite bandwidth required? No. Increasing bandwidth allows the system to react faster but also captures more noise and parasitic signals, such as those generated by switching power supplies. Therefore, it's essential to limit the bandwidth to what your application actually needs. Using an excessively wide bandwidth can reduce the system’s immunity to noise and compromise its robustness against external disturbances.
4.3-10 Connector,Mini Din To N Connector,4.3-10 To N Connector,4.3-10 Mini Din To N Conenctor
Changzhou Kingsun New Energy Technology Co., Ltd. , https://www.aioconn.com
